Acht oplossingen

De niet-transitiviteit van vriendschappen (ondanks het bekende gezegde dat de vrienden van mijn vrienden mijn vrienden zijn), dat een paar weken geleden werd geopperd , houdt duidelijk verband met de Soritesparadox. Want hoe klein ook, er is altijd een "afstand" (van ideeën, karakter, gedrag, enz.) tussen twee mensen. Een optelsom van nabijheid kan daarom een onoverbrugbare afstand worden, net zoals een winkel die zich vlakbij een winkel bevindt die zich vlakbij een winkel bevindt die zich vlakbij een winkel bevindt... die zich vlakbij je huis bevindt, zich aan de andere kant van de stad kan bevinden als we er maar genoeg nabijheid tussen plaatsen.

Wat betreft de acht kwesties van vorige week, een aantal snelle of slechts schetsmatige antwoorden en andere meer gedetailleerde:

1. Ons wordt verteld dat de vrouw geen donkere huid heeft, en de persoon met blond haar antwoordt dat ze dus wit haar moet hebben, dus...

2. Wat betreft het verdelen van de stompe driehoek in scherpe hoeken, is het gemakkelijk om tot de onjuiste conclusie te komen dat dit onmogelijk is (Martin Gardner zei dat hij in zijn tijd verschillende "demonstraties" van een dergelijke onmogelijkheid kreeg), want hoe ver we de driehoek ook verdelen, er blijft altijd minstens één kleine en hardnekkige stompe hoek over, zoals die in de rechterbenedenhoek van de afbeelding.

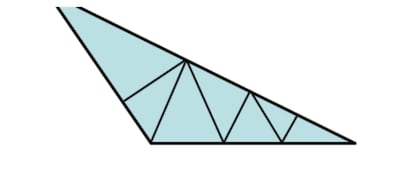
Delen is echter mogelijk, en als aanwijzing zou ik willen zeggen dat het een van die leerzame problemen is waarbij we onszelf onbewust meer voorwaarden opleggen dan ons wordt opgedragen. Wat is in dit geval de onbewuste, ongevraagde voorwaarde?

3. Er waren vijf Marx Brothers: Chico, Groucho, Harpo, Gummo en Zeppo; maar voor ons raadsel is de meest waarschijnlijke oplossing dat er vier waren (zoals in hun beroemdste films) en dat drie van hen linkshandig waren. De oplossing is niet uniek: er zouden ook 21 broers kunnen zijn, waarvan er 15 linkshandig zijn. Is er een andere oplossing, zelfs als die demografisch onwaarschijnlijk is?

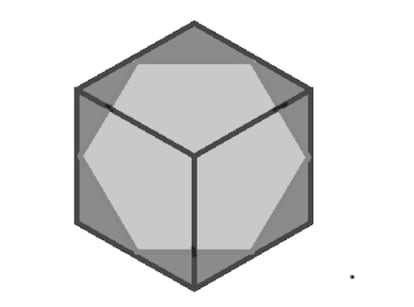
4. Als het snijvlak door de middens van zes ribben van de kubus gaat, verkrijgen we een regelmatige zeshoek.

5. 129 + 438 = 567 (Is deze oplossing uniek?).

6. Als OODDF de vierkantswortel van WONDERFUL is, kan O niet groter zijn dan 2, omdat het kwadraat tien cijfers zou hebben, en het kan niet 1 zijn, omdat het kwadraat van een getal beginnend met 11 geen 1 in het tweede cijfer kan hebben; daarom is O = 2. Het gezochte getal zal dus tussen de kwadraten van 22.000 en 23.000 liggen, en omdat het tweede cijfer van WONDERFUL 2 is, is W = 5… Door deze redenering te volgen, verkrijgen we WONDERFUL = 523.814.769.

7. De grootste cirkel die alleen door witte vierkanten gaat, heeft zijn middelpunt in het midden van een wit vierkant en gaat door de verst verwijderde hoekpunten van de vier zwarte vierkanten eromheen. (Wat is de straal?)

8. De treinen naderen met een relatieve snelheid van 130 + 170 = 300 km/u, dus 5 minuten voor de botsing zullen ze 25 km van elkaar verwijderd zijn. De oorspronkelijke afstand is irrelevant; die dient alleen maar om te misleiden.

Niet-transitieve spellen

Over non-transitiviteit merkte Salva Fuster op: "Niet-transitieve dobbelstenen zijn een van de meest verrassende gevallen die ik ken. Ik denk dat de meeste mensen die voor het eerst niet-transitieve dobbelstenen zien, proberen de fout te vinden door te tellen in hoeveel gevallen elke dobbelsteen een andere verslaat." Heel waar en interessant, zozeer zelfs dat een volgende blogpost de moeite waard is om aan dit onderwerp te wijden. En om je interesse te wekken, denk eens aan een ander niet-transitief spel. Er zijn er minstens twee erg populair...